NDLs vs. linear filters: an illustration
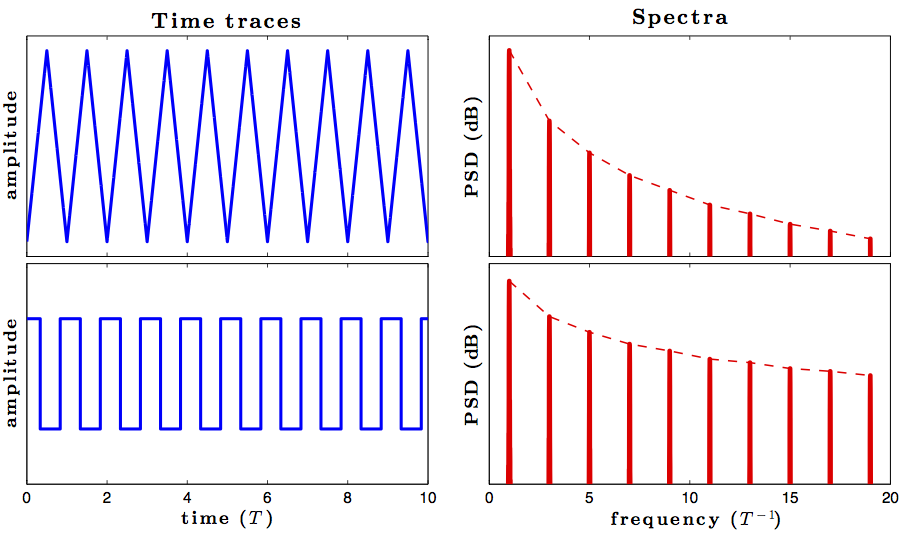
As a simplified example, let us consider triangle and square waves with some period T. Clearly, both waves consist of odd harmonics of the same fundamental frequency T−1, and thus their frequency spectra completely overlap. However, the frequencies are "coupled" differently for the triangle and the square waves, as can be seen from the relative powers of the harmonics in the figure below
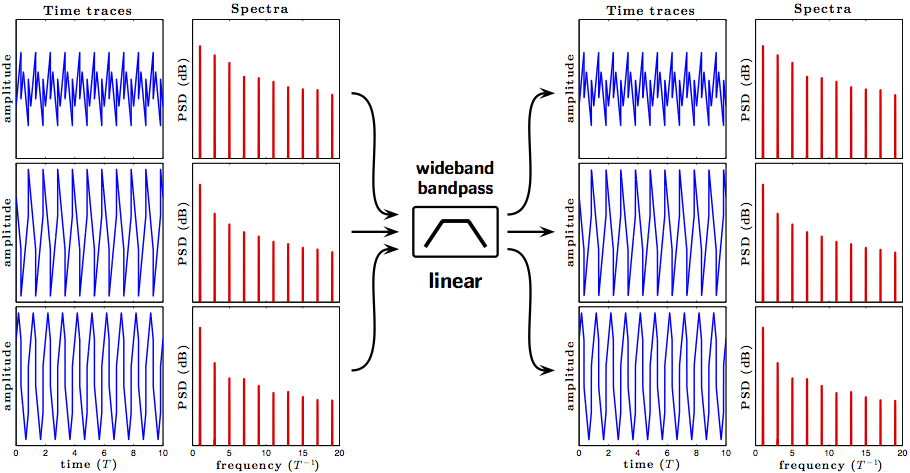
A sum of a triangle and a square waves will also consist of odd harmonics of the fundamental frequency T−1. The appearance of such a sum, and the power of the harmonics will depend on the magnitudes of both waves and on their phase relation, as can be seen in the figure below. A linear filter transparent to a triangle wave will also be transparent to a square wave, and vice versa, and will not be able to separate the two waves
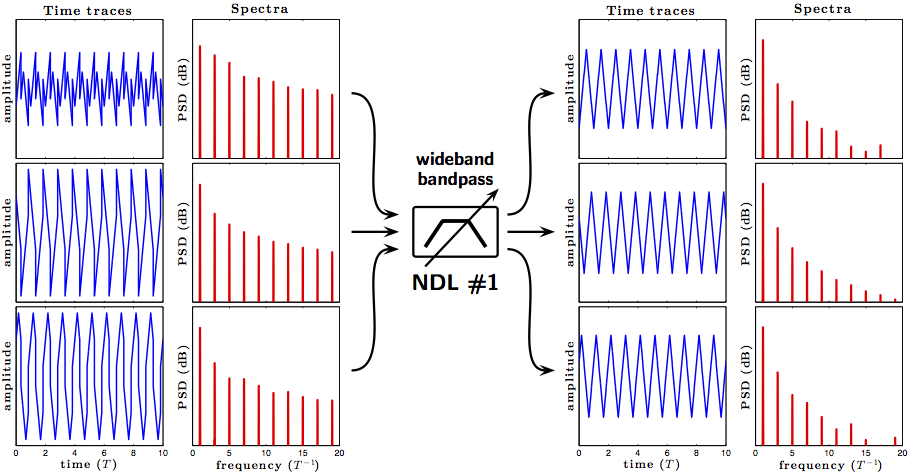
However, using the difference in the structure ("frequency coupling") between a triangle and a square waves, an NDL can be configured to be transparent to the triangle wave and to be opaque to the square wave, as illustrated in the figure below
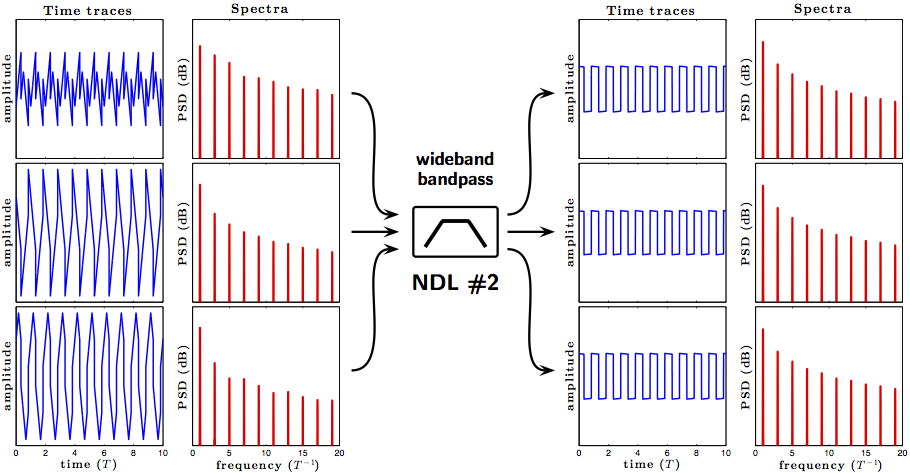
Contrariwise, an NDL can be configured to be transparent to a square wave and to be opaque to a triangle wave, as illustrated in the figure below
The following illustrative application demonstrates how the NDLs can increase resistance of communications receivers to man-made interference
